Math

Introduction

Math and reasoning remain as some of the most important unsolved problems for LLMs right now. However, existing public benchmarks such as GSM8k are widely believed to suffer from issues of data contamination. As part of a comprehensive evaluation of all aspects of a model’s capabilities, we have designed a new math and reasoning dataset called GSM1k. GSM1k is based on the popular GSM8k benchmark, aiming to mirror its problem distribution while introducing an entirely new set of questions. It contains a range of math problems that are approximately at the level of a fifth grade math exam. In this post, we present the methodology used to create GSM1k and a short preview of the results.

[math-data-1]

Dataset Description

Model evaluation is critical but tricky due to widespread concerns of data contamination. Because large language models are trained from data scraped from the web, many benchmarks that release all data publicly will find that some models perform artificially well due to models memorizing the eval set, or data distribution very similar to the eval set.

At Scale, we take the problem of data contamination very seriously. To measure the existing benchmark contamination on GSM8k, we created GSM1k, a held-out benchmark designed to match the difficulty and structure of GSM8k. To prevent models from overfitting on GSM1k, we’ve decided to publicly release only 50 samples from the 1,000 questions in this dataset. Although we still need to query different models to conduct the evaluations, the risk of overfitting can be reduced as long as model developers are mindful to avoid training their models on variations of this data.

To generate the dataset we screened 44 human annotators and asked them to generate a dataset of 1,000 problem sets. Each annotator received detailed guidelines and instructions on how to create the problem, and was assisted by a small team of operators to address any open questions. We carefully designed the GSM1k dataset such that it replicates the distribution and difficulty of the original GSM8k dataset. To ensure the data is correct and adheres to the guidelines, we employed 3 stages of quality validation: review layer, second solve, and independent audit (see details below). The fully completed set can now be utilized to evaluate on a standard basis the arithmetic competences of LLMs.

Dataset Construction

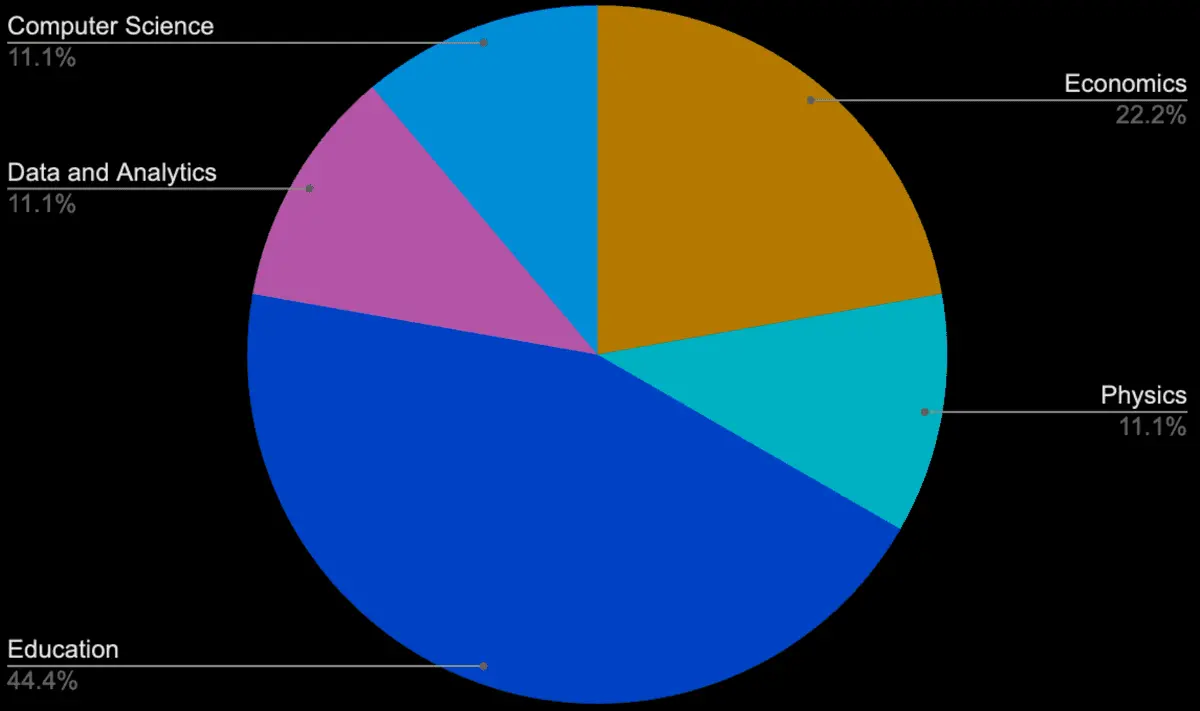
GSM1k was constructed over the span of 3 weeks with an annotator team that included grade school math educators and specialists with education, data and analytics, computer science, physics and economics background. We selected an annotator pool that was both qualified to generate these problems and that came from different backgrounds (see Annotators Background’ section). Data for GSM1k was collected through a five step process involving no LLM assistance. The steps included:

1. Initial data collection: Annotators were instructed to generate the new problem sets that required specific numbers of steps to solve.

2. Review layer: based on an initial review process executed by full-time experts on the team, the team identified a subset of trusted reviewers tasked with ensuring that problems were of the correct format, that the solutions were correct and that their difficulty levels were appropriately categorized.

3. Second Solve. In this step, we had an entirely different set of annotators solve a problem independently without access to the original answer. We discarded all problems that did not result in identical answers between the two solves.

4. Timed Difficulty Check. We asked a separate set of 20 annotators to solve as many problems as they could within 15 minutes. We analyzed the rate of correct responses to infer the level of difficulty of the problems they took. This step was done to ensure that GSM8k and GSM1k (ours) had comparable distributions of problems’ difficulty levels.

5. Distinguishability Check. In this step, we asked annotators to choose the “odd question out” when given 4 tasks randomly selected from GSM8k and 1 task randomly selected from GSM1k (ours). This was done to ensure that GSM1k was indistinguishable from GSM8k via human annotation.

By completing these five steps, we were able to create a set of original questions and answers mirroring the distribution of the original GSM8K dataset. Annotators of the problem sets were instructed to produce entirely unique Q&A pairs, devoid of assistance from chatbots or language models. This mandate extended to avoiding paraphrases or copies of existing problem sets publicly or privately available, with the goal of ensuring the prompts were original and human generated.

The instructions emphasized diversity not only in domains but also in the presentation of the problems (see Data Samples). Annotators were instructed to avoid repetition in problem settings, ensure solutions were positive integers or higher, and check that resolutions were consistent with the level of difficulty assigned to their specific problem.

Finally, the development process was underpinned by a set of rigorous quality control measures (see Quality Controls section), including the use of automated in-system checks to maintain grammatical standards and avoid inappropriate content.

Annotator Backgrounds

As part of annotator selection, we screened annotators on the basis of several criteria, including their accuracy, their prior track record and identified preferences. Once we identified a pool of candidates, we had live sessions with them to explain the prompt sets we wanted to create.

At the end of the process, we assembled a team of individuals with strong backgrounds in GSM mathematics. This team, comprising educators, mathematicians, and data scientists, brought a wealth of knowledge and expertise to the project. Their role was multifaceted: from designing the diverse array of math prompts to reviewing the llm-generated responses.

Quality Controls

To enhance the quality and reliability of the Scale AI Math Prompts Set, we've adopted a comprehensive quality assurance (QA) strategy. This includes 3 layers of review after initial attempts, and multiple quality assessments to address all aspects of dataset quality and diversity. Our final quality control was performed by an independent internal quality auditor, which reviewed all 1k prompts against the original guidelines.

Evaluation Methodology

We use a fork of lm-evaluation-harness with 5-shot examples drawn from GSM8k to ensure consistency and comparability across models. More details can be found in our paper. While the evaluation conducted in our paper was fully automated, for the leaderboard evaluation, we additionally use human annotation to select the final answer manually to ensure that this leaderboard measures mathematical ability instead of also testing for following the proper instruction format. As such, unlike the fully automated GSM1k evaluation used in the paper, this leaderboard does not penalize a model who outputs the correct answer but not in the same format as the few-shot examples. As a result, all accuracies in the final rankings are higher than those used in the paper, with some models, such as Claude 3 Opus, showing substantial jumps due to “chattiness’’ in their answer formatting.

Acknowledgments

This project was made possible by the dedicated efforts of a team of experts in AI, mathematics, and dataset creation. We extend our gratitude to everyone involved in the development and refinement of the dataset and the verification methodology.

Scale AI Team: Vaughn Robinson*, Hugh Zhang*, Mike Lunati, Dean Lee, Daniel Berrios, William Qian, Kenneth Murphy, Summer Yue

Appendix

Background of the Annotators (Percent)